Ncert Solution Class 12 Chemistry Chapter 1

Ncert Class 12: Chemistry Chapter 1 The Solid State

---

Solutions of Class 12 Chapter 1 Chemistry:-

Ncert Exercises

1.1. Define the term 'amorphous'. Give a few examples of amorphous solids.

Solution:

Amorphous solids are those substances, wherein there is no regular arrangement of its constituent particles, (i.e., particles, atoms or atoms). The arrangement of the establishing particles has just short-range request, i.e., a regular and periodically repeating pattern is seen over brief distances just, e.g., glass, elastic, and plastics.

1.2. What makes glass different from a solid such as quartz? Under what conditions could quartz be converted into glass?

Solution:

Glass is a supercooled fluid and an amorphous substance. Quartz is the crystalline type of silica (SiO2) in which tetrahedral units SiO4 are connected with each other in such a way that the oxygen atom of one tetrahedron is shared with another Si atom. Quartz can be converted into glass by softening it and cooling the dissolve rapidly. In the glass, SiO4 tetrahedra are participated in a random manner.

1.3 Classify each of the following solids as ionic, metallic, modular, network (covalent), or amorphous:

(i) Tetra phosphorus decoxide (P4O10) (ii) Ammonium phosphate, (NH4)3PO4 (iii) SiC (iv) I2 (v) P4 (vii) Graphite (viii), Brass (ix) Rb (x) LiBr (xi) Si

Solution:

Metallic : ( h ) Brass, ( i ) Rb

Molecular : (a) Tetra phosphorus decaoxide (P4O10), (d) I2, (e) P4.

Ionic : ( b ) Ammonium phosphate (NH4)3PO4, ( j ) LiBr

Amorphous : ( f ) Plastic

Covalent : ( c ) SiC, ( g ) Graphite, ( k ) Si

1.4 (i) What is meant by the term 'coordination number'?

(ii) What is the coordination number of atom

(a) in a cubic close-packed structure?

(b) in a body focused cubic structure?

Solution:

(i) The number of nearest neighbors of a particle are called its coordination number.

(ii) (a) 12 (b) 8

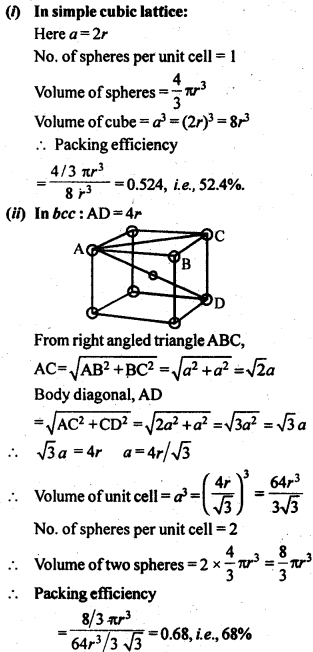
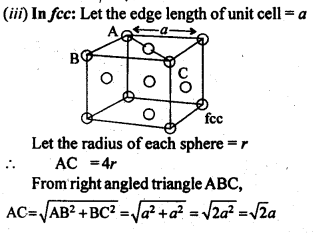
1.5. How can you determine the atomic mass of an unknown metal if you know its density and dimensions of its unit cell ? Explain your answer.

Solution:

Given,
We know the aspect and thickness of its unit cell.
Let,
The edge length of a unit cell = a
The volume of the cell = a³
Thickness = d
Nuclear mass = M
Mass of unit cell = No. of particles in unit cell x Mass of every molecule = Z × m
Mass of a particle present in the unit cell, m = M/Na
where Na is the Avogadro's number.
We know,
d = Mass of unit cell/Volume of unit cell = Zm/a³ = Z.M/a³Na
Consequently, Atomic mass, M =( da³ Na)/Z

1.6 'Stability of a crystal is reflected in the magnitude of its melting points'. Comment. Collect melting points of solid water, ethyl alcohol, diethyl ether and methane from a data book. What can you say about the intermolecular forces between these molecules?

Solution:

Higher the melting point, greater are the forces holding the constituent particles together and consequently greater is the stability of a crystal. It are following to Melt points of given substances. Water = 273 K, Ethyl alcohol = 155.7 K, Diethylether = 156.8 K, Methane = 90.5 K.

The intermoleoilar forces present in case of water and ethyl alcohol are mainly because of the hydrogen bonding which is answerable for their high melting points. Hydrogen bonding is more grounded in case of water than ethyl alcohol and henceforth water has higher melting point then ethyl alcohol. Dipole-dipole interactions are available in case of diethylether. The main forces present in case of methane is the weak van der Waal's forces (or London dispersion forces).

1.7. How will you distinguish between the following pairs of terms :

(a) Hexagonal close packing and cubic close packing

(b) Crystal lattice and unit cell

(c) Tetrahedral void and octahedral void.

Solution:

(a) In hexagonal close pressing (hcp), the circles of the third layer are upward over the circles of the principal layer

(ABABAB… … . type). Then again, in cubic close pressing (ccp), the circles of the fourth layer are available over the circles of the principal layer (ABCABC… ..type).

(b) Unit cell: It is the littlest 3D layered part of a total space grid, which when rehashed again and again this way and that from the gem cross section.

Gem grid - it is a normal direction of particles of a gem in a 3D space.

(c) Octahedral void - it is a void encircled by 6 circles.

Tetrahedral void - it is a void encircled by 4 circles.

1.8 How many lattice points are there is one unit cell of each of the following lattices?

(i) Face focused cubic (if) Face focused tetragonal (iii) Body focused cubic

Solution:

1.9 Explain:

(i) The basis of similarities and differences between metallic and ionic crystals.

(ii) Ionic solids are hard and brittle.

Solution:

(I) Similarities : Both ionic and metallic precious stones have electrostatic powers of fascination. In ionic precious stones, these are between the oppositely charged particles. In metals, these are among the valence electrons and the bits. That is the reason both have non-directional bonds.

Contrasts : (a) In ionic precious stones, the particles are not allowed to move. Thus, they can't lead power in the strong state. They can do so just in the liquid state or in fluid arrangement. In metals, the valence electrons are allowed to move. Thus, they can direct power in the strong state.

(b) Ionic bond is solid because of electrostatic powers of fascination. Metallic bond might be feeble or solid relying on the quantity of valence electrons and the size of the parts.

(ii) Ionic gems are hard in light of the fact that they have solid electrostatic powers of fascination among the oppositely charged particles. They are fragile on the grounds that ionic bond is non-directional.

1.10 Calculate the efficiency of packing in case of a metal crystal for (i) simple cubic, (ii) body focused cubic, and (iii) face focused cubic (with the assumptions that atoms are touching each other).

Solution:

Packing efficiency: It is the percentage of total space filled by the particles.

1.11 Silver solidifies in fcc lattice. If edge length of the cell is 4.07 x 10-8 cm and density is 10.5 g cm-3, calculate the atomic mass of silver.

Solution:

1.12. A cubic solid is made of two elements P and Q. Atoms Q are at the corners of the cube and P at the body place. What is the formula of the compound ? What is the co-ordination number of P and Q?

Solution:

Contribution by atoms Q present at the eight corners of the cube = \(\frac{1}{8}\) x 8 = 1

Contribution by atom P present at the body place = 1

Thus, P and Q are present in the ratio 1:1.

∴ Formula of the compound is PQ.

Co-ordination number of atoms P and Q = 8.

1.13 Niobium crystallizes in a body focused cubic structure. If density is 8.55 g cm-3, calculate atomic radius of niobium, it its atomic mass 93u to use.

Solution:

1.14 If the radius of the octahedral void is r and radius of the atoms in close-packing is R, derive relation between rand R.

Solution:

R and r are the radii of the octahedral site and atoms respectively, then from Pythagoras theorem we get

\(AC^2\) = \(AB^2\) + \(BC^2\)

\(2R^2\) = \((R+r)^2\) + \((R+r)^2\)

or,\(\sqrt{2}\)R = R+r

or,(\(\sqrt{2}\)-1)R = r

∴ r = 0.414 R

1.15 Copper crystallizes into a fee lattice with edge length 3.61 x 10-8 cm. Show that the calculated density is in agreement with its measured value of 8.92 gcm-3.

Solution:

This calculated value of density is closely in agreement with its measured value of 8.92 g cm3.

1.16 Analysis shows that nickel oxide has the formula \(Ni_{0.98}\) \(O_{1.00}\). What fractions of nickel exist as \(Ni^{2+}\) and \(Ni^{3+}\) ions?

Solution:

98 Ni-atoms are associated with 100 O - atoms. Out of 98 Ni-atoms, suppose Ni present as \(Ni^{2+}\) = x

Then Ni present as  \(Ni^{3+}\) = 98 - x

Total charge on x  \(Ni^{2+}\) and (98 - x)  \(Ni^{3+}\) should

be equal to charge on 100 \(O^{2-}\)ions.

Hence, x × 2 + (98 - x) × 3 = 100 × 2 or 2x + 294 - 3x = 200 or x = 94

∴ Fraction of Ni present as \(Ni^{2+}\) = \(\frac{94}{98}\) × 100 = 96%

Fraction of Ni present as \(Ni^{3+}\) = \(\frac{4}{98}\) × 100 = 4%

1.17 What are semi-conductors? Describe the two main types of semiconductors and contrast their conduction mechanisms.

Solution:

Semi-conductors are the substances whose conductivity lies in between those of conductors and insulators. The two

main types of semiconductors are n-type and p-type.

(i) n-type semiconductor: When a silicon or germanium crystal is doped with group 15 element like P or As, the dopant atom forms four covalent bonds like Si or Ge atom but the fifth electron, not used in bonding, becomes delocalised and continues its share towards electrical conduction. Thus silicon or germanium doped with P or As is called H-type semiconductor, a-indicative of negative since it is the electron that conducts electricity.

(ii) p-type semiconductor: When a silicon or germanium is doped with group 13 element like B or Al, the dopant is present only with three valence electrons. An electron vacancy or a hole is created at the place of missing fourth electron. Here, this hole moves throughout the crystal like a positive charge giving rise to electrical conductivity. Thus Si or Ge doped with B or Al is called p-type semiconductor, p stands for positive hole, since it is the positive hole that is responsible for conduction.

1.18 Non-stoichiometric cuprous oxide, Cu2O can be prepared in laboratory. In this oxide, copper to oxygen ratio is slightly less than 2:1. Can you account for the fact that this substance is a p-type semiconductor?

Solution:

The ratio less than 2 : 1 in \(Cu_2\)0 shows cuprous (\(Cu^+\)) particles have been replaced by cupric (\(Cu^{2+}\)) particles. For maintaining electrical neutrality, each two \(Cu^+\) particles will be replaced by one \(Cu^{2+}\) particle thereby creating an opening. As conduction will be because of the presence of these positive openings, thus it is a p-type semiconductor.

1.19 Ferric oxide crystallizes in a hexagonal dose-packed array of oxide ions with two out of every three octahedral holes occupied by ferric ions. Derive the formula of the ferric oxide.

Solution:

Suppose the number of oxide ions (\(O^{2-}\)) in the packing = 90

∴ Number of octahedral voids = 90

As \(2/3^{rd}\) of the octahedral voids are occupied by ferric ions, therefore, number of ferric ions 2 present = \(\frac{2}{3}\) × 90 = 60

∴ Ratio of \(Fe^{3+}\) : \(O^{2-}\)= 60 : 90 = 2 : 3

Hence, the formula of ferric oxide is \(Fe_{2}O_{3}\).

1.20 Classify each of the following as being either a p-type or n-type semiconductor :

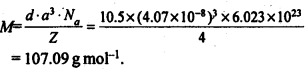
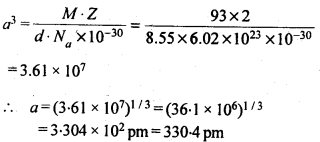
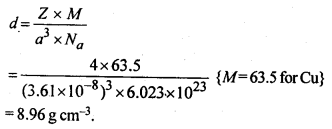
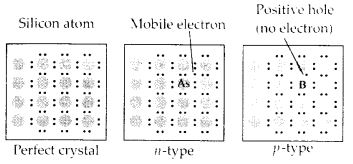
1. Ge doped with In
2. B doped with Si.

Solution:

1. Ge is group 14 element and In is group 13 element. Hence, an electron deficient hole is created and therefore, it is a p - type semiconductor.
2. B is group 13 element and Si is group 14 element, there will be a free electron, So, it is a n-type semiconductor.

1.21 Gold (atomic radius = 0.144 nm) crystallizes in a face focused unit cell. What is the length of the side of the unit cell ?

Solution:

For a face centered cubic unit cell (fcc)

Edge length (a) = \(2\sqrt{2}\)r = 2 x 1.4142 x 0.144 mm = 0.407 nm

1.22 In terms of band theory, what is the difference

1. between a conductor and an insulator
2. between a conductor and a semiconductor?

Solution:

In most of the solids and in many insulating solids conduction takes place due to migration of electrons under the influence of electric field. However, in ionic solids, it is the ions that are responsible for the conducting behavior due to their movement.

(i) In metals, conductivity strongly depends upon the number of valence electrons available in an atom. The atomic orbitals of metal atoms form molecular orbitals which are so close in energy to each other, as to form a band. If this band is partially filled or it overlaps with the higher energy unoccupied conduction band, then electrons can flow easily under an applied electric field and the metal behaves as a conductor.

If the gap between valence band and next higher unoccupied conduction band is large, electrons cannot jump into it and such a substance behaves as insulator.

(ii) If the gap between the valence band and conduction band is small, some electrons may jump from valence band to the conduction band. Such a substance shows some conductivity and it behaves as a semiconductor. Electrical conductivity of semiconductors increases with increase in temperature, since more electrons can jump to the conduction band. Silicon and germanium show this type of behavior and are called intrinsic semiconductors. Conductors have no forbidden band.

1.23 Explain the following terms with suitable examples :

1. Schottky defect
2. Frenkel defect
3. Interstitial defect
4. F-focuses.

Solution:

(i) Schottky defect : In Schottky defect a pair of vacancies or holes exist in the crystal lattice due to the absence of equal number of cations and anions from their lattice points. It is a common defect in ionic compounds of high coordination number where both cations and anions are of the same size, e.g., KCl, NaCl, KBr, etc. Due to this defect density of crystal decreases and it begins to conduct electricity to a smaller extent.

(ii) Frenkel defect : This defect arises when some of the ions in the lattice occupy interstitial sites leaving lattice sites vacant. This defect is generally found in ionic crystals where anion is much larger in size than the cation, e.g., AgBr, ZnS, etc. Due to this defect density does not change, electrical conductivity increases to a small extent and there is no change in overall chemical composition of the crystal.

(iii) Interstitial defect : When some constituent particles (atoms or molecules) occupy an interstitial site of the crystal, it is said to have interstitial defect. Due to this defect the density of the substance increases.

(iv) F-Centers : These are the anionic sites occupied by unpaired electrons. F-focuses impart color to crystals. The color results by the excitation of electrons when they absorb energy from the visible light falling on the crystal.

1.24 Aluminum crystallizes in a cubic close packed structure. Its metallic radius is 125 pm.

1. What is the length of the side of the unit cell?
2. How many unit cells are there in 1.00 cm3 of aluminum?

Solution:

1.25 If NaCI is doped with \(10^{-3}\) mol % \(SrCl_{2}\), what is the concentration of cation vacancies ?

Solution:

Let moles of NaCI = 100
∴ Moles of \(SrCl_{2}\) doped = \(10^{-3}\)
Each \(Sr^{2+}\) will replace two \(Na^{+}\) ions. To maintain electrical neutrality it occupies one position and thus creates one cation vacancy.
∴ Moles of cation vacancy in 100 moles NaCI = \(10^{-3}\)
Moles of cation vacancy in one mole
NaCI = \(10^{-3}\) × \(10^{-2}\) = \(10^{-5}\)
∴ Number of cation vacancies
= \(10^{-5}\) × 6.022 × \(10^{23}\) = 6.022 × \(10^{18} mol^{-1}\)

1.26 Explain the following with suitable example:

1. Ferromagnetism
2. Paramagnetism
3. Ferrimagnetism
4. Antiferromagnetism
5. 12-16 and 13-15 group compounds.

Solution:

(i) Ferromagnetic substances : Substances which are attracted very strongly by a magnetic field are called ferromagnetic substances, e.g., Fe, Ni, Co and \(CrO^{2}\) show ferromagnetism. Such substances remain permanently magnetized, once they have been magnetized. This type of magnetic moments are due to unpaired electrons in the same direction.

The ferromagnetic material, \(CrO^{2}\), is used to make magnetic tapes used for audio recording.

(ii) Paramagnetic substances : Substances which are weakly attracted by the external magnetic field are called paramagnetic substances. The property thus exhibited is called paramagnetism. They are magnetized in the same direction as that of the applied field. This property is shown by those substances whose atoms, ions or molecules contain unpaired electrons, e.g., \(O_{2}\), \(Cu^{2+}\), \(Fe^{3+}\), etc. These substances, however, lose their magnetism in the absence of the magnetic field.

(iii) Ferrimagnetic substances : Substances which are expected to possess large magnetism on the basis of the unpaired electrons but actually have small net magnetic moment are called ferrimagnetic substances, e.g., \(Fe_{3}O_{4}\), ferrites of the formula \(M^{2+}Fe_{2}O_{4}\) where M = Mg, Cu, Zn, etc. Ferrimagnetism arises due to the unequal number of magnetic moments in opposite direction resulting in some net magnetic moment.

(iv) Antiferromagnetic substances : Substances which are expected to possess paramagnetism or ferromagnetism on the basis of unpaired electrons but actually they possess zero net magnetic moment are called antiferromagnetic substances, e.g., MnO. Antiferromagnetism is due to the presence of equal number of magnetic moments in the opposite directions.

(v) 13-15 group compounds : When the solid state materials are produced by combination of elements of groups 13 and 15, the compounds thus obtained are called 13-15 compounds. For example, InSb, AlP, GaAs, etc.

12-16 group compounds : Combination of elements of groups 12 and 16 yield some solid compounds which are referred to as 12-16 compounds. For example, ZnS, CdS, CdSe, HgTe, etc. In these compounds, the bonds have ionic character.

**END**